
Italian voiceover of How Bitcoin Works (by Simone Falcini)
Spanish Translation (by Diego J Martinez Garcia)
Intro
The goal of this video is to explain how Bitcoin works under the hood, to give a clearer idea of what it really means to own, send or “mine” Bitcoins.
If, instead of how it works, you're looking for where to buy Bitcoin, I use coinbase. And for trading, check out bitcoin wealth alliance (both affiliate links).
What is Bitcoin at a high level?
First, a brief high-level overview of what Bitcoin is.

At its core, Bitcoin is just a digital file that lists accounts and money like a ledger. A copy of this file is maintained on every computer in the Bitcoin network. (update: you don't have to maintain a ledger just to use Bitcoin to send and receive money, this is for people who want to help maintain the system).

These numbers don’t represent anything in the physical world, they only have value because people are willing to trade real goods and services for a higher number next to their account, and believe that others will do the same. The numbers only have value because we believe they have value, just like any other fiat currency.
To send money, you broadcast to the network that the amount on your account should go down, and the amount on a receiver’s account up. Nodes, or computers, in the Bitcoin network apply that transaction to their copy of the ledger, and then pass on the transaction to other nodes. This, with some math-based security, is really all there is--a system that lets a group of computers maintain a ledger.
While this may sound similar to the way a bank maintains a ledger, the fact that the ledger is maintained by a group rather than a single entity introduces a number of important differences. For one, unlike at a bank where you only know about your own transactions, in Bitcoin, everyone knows about everyone else’s transactions.
Also, while you can trust your bank, or can at least sue it if something goes wrong, in Bitcoin, you’re dealing with anonymous strangers, so you shouldn’t trust anyone. The Bitcoin system is amazingly designed so that no trust is needed--special mathematical functions protect every aspect of the system.
The rest of this entry will explain in detail how Bitcoin allows such a group of strangers to manage each other’s financial transactions.
How Sending Money in Bitcoin Works
At a basic level, for Alice to send money to Bob, she simply broadcasts a message with the accounts and the amount:
“Send 5.0 BTC from Alice to Bob.”
Every node that receives it will update their copy of the ledger, and then pass along the transaction message. But how can the nodes be sure that the request is authentic, that only the rightful owner has sent the message?
Bitcoin rules require a kind of password to unlock and spend funds, and this password is what’s called a “Digital Signature.” Like a real handwritten signature, it proves the authenticity of a message, but it does so through a mathematical algorithm that prevents copying or forgery in the digital realm.
Unlike a simple static password, a completely different Digital Signature is required for every transaction. Keep in mind that in Bitcoin, you’re dealing with complete strangers, so you never want to reveal a password that could be copied and reused by someone else.
A Digital Signature works by utilizing two different (but connected) keys, a “private key” to create a signature, and a “public key” that others can use to check it.
You can think of the private key as the true password, and the signature as an intermediary that proves you have the password without requiring you to reveal it.
Public keys are actually the “send to” addresses in Bitcoin, so when you send someone money, you’re really sending it to their public key.
To spend money, you must prove that you’re the true owner of a public key address where money was sent, and you do that by generating a Digital Signature from a transaction message and your private key.
signature = f(message, private key)
Other nodes in the network can use that signature in a different function to verify that it corresponds with your public key.
1 =? v(message, public key, signature)
Through the math behind the Digital Signature, they are able to verify that the sender owned a private key without actually seeing it.
Importantly, because the signature depends on the message, it will be different for every transaction, and therefore can’t be reused by someone for a different transaction. This dependence on the message also means that no one can modify the message while passing it along the network, as any changes to the message would invalidate the signature.
The math behind this is fairly complex, and while I won’t try to explain it fully now, here are some topics you can google to get started: ECDSA and mathematical trap door. More at the end of the video.
Bitcoin Transactions and Ledger in Detail
So far, we know that Digital Signatures are used to ensure a transaction is authorized, but I’ve over-simplified how nodes in the network keep track of account balances. In fact, no records of account balances are kept at all. If you don’t keep track of how much money any given person has, how do you know if they have enough to send to someone else?
Instead of balances, ownership of funds is verified through links to previous transactions. Here’s how this works.
To send 5.0 BTC to Bob, Alice must reference other transactions where she received 5 or more Bitcoins. These referenced transactions are called “inputs.” Other nodes verifying this transaction will check those inputs to make sure Alice was in fact the recipient, and also that the inputs add up to 5 or more Bitcoins.
Let’s look at a real transaction to see this in practice.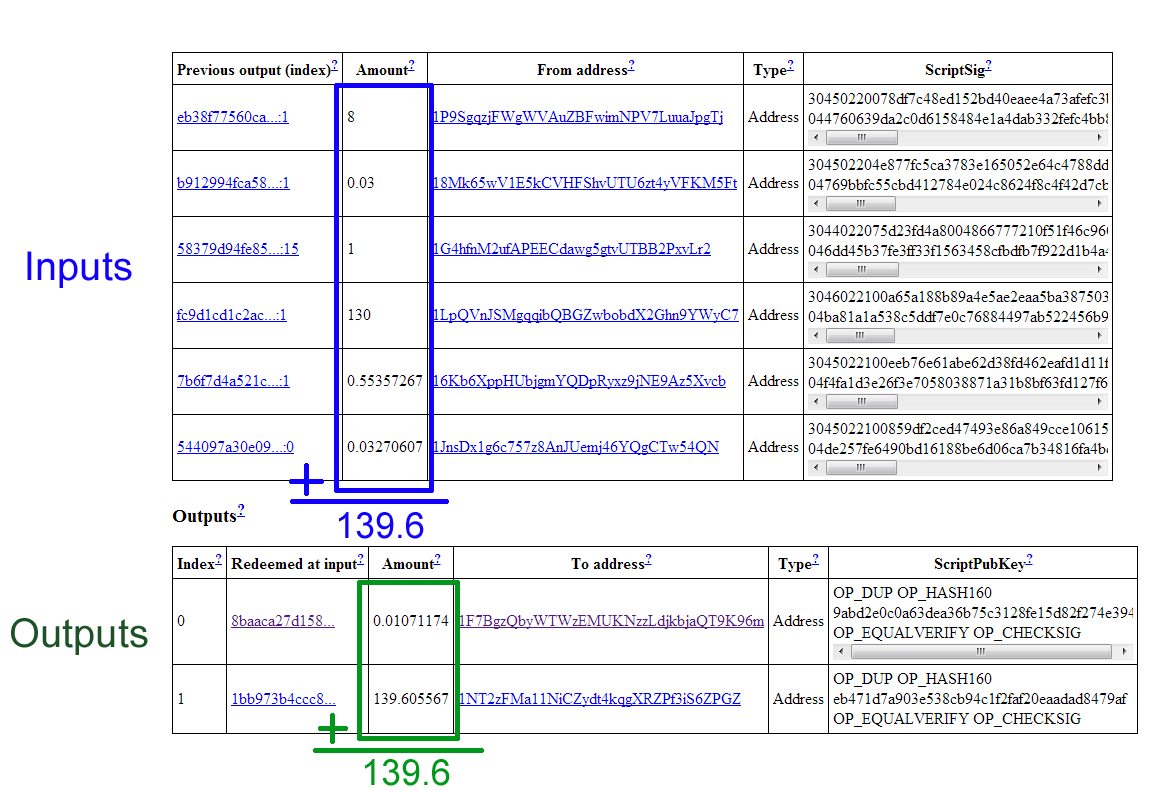
This transaction references 6 inputs for a total of 139.6 Bitcoins. In the output section, notice that there are two lines. The first one of these is actually going back to the sender as change for the transaction. A simplifying rule states that each input must be used up completely in a transaction, so if you’re trying to send an amount that doesn’t exactly match one of your inputs, you need to send any remaining amount back to yourself.
Through these referenced input linkages, ownership of Bitcoins is passed along in a kind of chain, where the validity of each transaction is dependent on previous transactions. But how can you trust those previous transactions? You can’t, and should check their inputs, too. In fact, when you first install Bitcoin wallet software, it downloads every transaction ever made, and checks each one’s validity all the way back to the first transaction ever made. Remember, you’re dealing with complete strangers, so it’s important to verify every transaction yourself. This process can take over 24 hours, but only needs to be done once.
Once a transaction has been used once, it is considered spent, and cannot be used again. Otherwise, someone could double-spend an input by referencing it in multiple transactions. So, when verifying a transaction, in addition to the other checks, nodes also make sure the inputs haven’t already been spent. To be explicit, for each input, nodes check every other transaction ever made to make sure that input hasn’t already been used before. While this may seem time consuming, as there are now over 20 million transactions, it’s made fast with an index of unspent transactions.
So, instead of a ledger of balances, Bitcoin nodes keep track of a giant list of transactions. Owning Bitcoins means that there are transactions in this list that point to your name, and haven’t been spent, or, in other words, used as inputs in other transactions.
One interesting consequence of this ownership structure is that figuring out your own balance requires iterating through every transaction ever made and adding up all your unspent inputs.
Another interesting note about transactions is that the system can support more complex ones than simply sending funds to one person. You may have noticed a cryptic looking line of text in the output shown previously.
OP_DUP OP_HASH160 9abd2e0c0a63dea36b75c3128fe15d82f274e394 OP_EQUALVERIFY OP_CHECKSIG
It turns out that outputs are more like puzzles to be solved rather than simple “to addresses.” Rather than emailing, sending money in Bitcoin is more like putting money in a public locker and attaching a math puzzle that must be solved to open it. The puzzle is defined using a special scripting language, and while it’s typically designed so that only a single owner of a public key can solve it, more complex conditions are possible. For instance, 2 out of 3 signatures could be required for an escrow based transaction. Another example is the very first bitcoin transaction ever made, which was a puzzle that anyone could solve.
While most Wallet software hides this scripting layer for you, you’re free to write your own software and claim conditions, although this can be risky. Over 2600 BTC were lost in one batch of transactions due to a malformed address.
This highlights an important part of Bitcoin. As there is no bank or credit card company you can appeal to, any “user-error” mistakes can result in the permanent loss of Bitcoins, not just from your own account, but from the Bitcoin economy overall. If you lose your private key, any funds associated with the corresponding public key will be gone forever. Because people will likely lose private keys due to hard drive crashes and insufficient backups, this means the Bitcoin currency will eventually be a deflationary one.
Anonymity
Before explaining the final piece that secures Bitcoin (“mining”), I want to highlight a few points about anonymity in Bitcoin.
If you access Bitcoin through a TOR network that hides your IP address, you can use Bitcoin without ever revealing anything more than your public key. And to avoid someone linking your transactions together (remember, they’re all publicly stored on every computer!), you can generate a new public key for every incoming transaction.
If you access Bitcoin through a TOR network that hides your IP address, you can use Bitcoin without ever revealing anything more than your public key. And to avoid someone linking your transactions together (remember, they’re all publicly stored on every computer!), you can generate a new public key for every incoming transaction.
 |
| Bitcoin transaction that combines public keys |
You might think that generating a public key “receiving address” could potentially create a link to your true identity, but even this step is anonymous, and amazingly, can be done with no connection to the network. You simply click a button in your Wallet software, and it randomly generates a new private and public key. Because there are so many different possible addresses, there’s no reason to even check if someone else already has that key (compare this to signing up for an email address, where almost everything you might try has been taken). In fact, if you did guess someone else’s key, you would have access to their money!
This is the total number of possible Bitcoin addresses:
1461501637330902918203684832716283019655932542976 (1.46 x 10^48 or 2^160)
These large numbers protect the Bitcoin system in several ways, so it’s useful to try to appreciate just how big they are. Some estimates for the number of grains of sand in the entire world are around 7.5 x 10^18th, or 7,500,000,000,000,000,000. Now imagine that every grain of sand represented an entire other Earth of additional grains, and you’re still much smaller than the possible number of Bitcoin addresses.
(strictly speaking, the probability of two addresses matching gets reduced as the number of users increases due to the Birthday Problem, but we’re still in the 2.9 x 10^39 range with a billion addresses).
http://www.hawaii.edu/suremath/jsand.html
Double Spending in Bitcoin
Let’s recap Bitcoin security so far. By verifying the Digital Signature, we know that only the true owner could have created the transaction message. And to make sure the sender actually has money to spend, we also check each referenced input, making sure it is unspent. But there is still one large security hole in the system that can make this “unspent check” unreliable, and this has to do with the order of transactions.
Considering that transactions are passed node-by-node through the network, there’s no guarantee that the order in which you receive them represents the order in which they were created. And you shouldn’t trust a timestamp because one could easily lie about the time a transaction was created. (Contrast this with a centralized system like paypal, where it’s easy for a central computer to keep track of the order of transactions.)
Considering that transactions are passed node-by-node through the network, there’s no guarantee that the order in which you receive them represents the order in which they were created. And you shouldn’t trust a timestamp because one could easily lie about the time a transaction was created. (Contrast this with a centralized system like paypal, where it’s easy for a central computer to keep track of the order of transactions.)
Therefore, you have no way to tell whether one transaction came before another, and this opens up the potential for fraud. A malicious user, Alice, could send a transaction giving money to Bob, wait for Bob to ship a product, and then send another transaction referencing the same “input” back to herself.
Because of differences in propagation times, some nodes on the network would receive the 2nd “double-spending” transaction before the one to Bob. And when Bob’s transaction arrived, they would consider it invalid because it’s trying to re-use an input. So Bob would be out both his shipped product and his money. Overall, there would be disagreement across the network about whether Bob or Alice had the money, because there’s no way to prove which transaction came first.
Because of differences in propagation times, some nodes on the network would receive the 2nd “double-spending” transaction before the one to Bob. And when Bob’s transaction arrived, they would consider it invalid because it’s trying to re-use an input. So Bob would be out both his shipped product and his money. Overall, there would be disagreement across the network about whether Bob or Alice had the money, because there’s no way to prove which transaction came first.
In light of this, there needs to be a way for the entire network to agree about the order of transactions, which is very much a daunting challenge in a decentralized system. Bitcoin’s solution is a clever way to both determine and safeguard the ordering through a kind of mathematical race.
The Block Chain: an Ordering of Transactions
The Bitcoin system orders transactions by placing them in groups called blocks, and linking those blocks together in something called the block chain. Note that this is different from the transaction chain we discussed earlier. The block chain is used to order transaction, whereas the transaction chain keeps track of how ownership changes.
Any node can collect a set of unconfirmed transactions into a block, and broadcast it to the rest of the network as a suggestion for what the next block in the chain should be. Because multiple people could create blocks at the same time, there could be several options to choose from, so how does the network decide which should be next? We can’t rely on the order that blocks arrive, because, as explained with transactions above, they may arrive in different orders at different points in the network.
Part of Bitcoin’s solution is that each valid block must contain the answer to a very special mathematical problem. Computers run the entire text of a block plus an additional random guess through something called a cryptographic hash until the output is below a certain threshold.
A hash function creates a short digest from any arbitrary length of text, in our case, the result is a 32 byte number. Here are some examples of the specific hash function Bitcoin uses, SHA256:
SHA256(“short sentence”)
0x 0acdf28f4e8b00b399d89ca51f07fef34708e729ae15e85429c5b0f403295cc9
SHA256("The quick brown fox jumps over the lazy dog")
0x d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592
SHA256("The quick brown fox jumps over the lazy dog.") (extra period added)
0x ef537f25c895bfa782526529a9b63d97aa631564d5d789c2b765448c8635fb6c
0x d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592
SHA256("The quick brown fox jumps over the lazy dog.") (extra period added)
0x ef537f25c895bfa782526529a9b63d97aa631564d5d789c2b765448c8635fb6c
Note how much the output changes in result of a single extra period at the end of the third example. The output is completely unpredictable, so the only way to find a particular output value is to make random guesses. It’s very much like guessing the combination to a lock. You might get lucky on your first guess, but on average, it takes many guesses. In fact, it would take a typical computer several years of guessing to solve a block.
With every computer in the entire Bitcoin network all guessing numbers, it takes about 10 minutes on average for someone to find a solution.
The first person to solve the math problem broadcasts their block, and gets to have their group of transactions accepted as next in the chain. The randomness in the math problem effectively spreads out when people find a solution, making it unlikely that two people will solve it at the same time.
Occasionally, however, more than one block will be solved at the same time, leading to several possible branches.
Occasionally, however, more than one block will be solved at the same time, leading to several possible branches.
In this case, you simply build on top of the first one you received. Others may have received the blocks in a different order, and will be building on the first block they received.
The tie gets broken when someone solves another block. The general rule is that you always immediately switch to the longest branch available. The math makes it rare for blocks to be solved at the same time, and even more rare for this to happen multiple times in a row. The end result is that the block chain quickly stabilizes, meaning that everyone is in agreement about the ordering of blocks a few back from the end of the chain.
Double Spending in the Block Chain
The fact that there’s some ambiguity in the end of the chain has some important implications for transaction security. For instance, if your transaction finds itself in one of the shorter branches, it will lose its place in line within the block chain. Typically, this means it will just go back into the pool of unconfirmed transactions, and be included in a later block. Unfortunately, this potential for transactions to lose their place opens the door to the very double-spend attack that was our original motivation for an ordering system.
Let’s look at how a double spend attack would work in the system described so far. A fraudster, Alice, sends money to Bob. Bob then waits for the transaction to get “confirmed” into the block chain, and then ships a product.
Now, because nodes always switch to a longer branch, if Alice can generate a longer branch that replaces the transaction to Bob with one to someone else, his money will effectively get erased.
Bob’s transaction will initially get tossed back into the unconfirmed pool. But since Alice has replaced it with another transaction that uses its same input, nodes will now consider Bob’s transaction invalid, because it’s referencing an already spent input.
Bob’s transaction will initially get tossed back into the unconfirmed pool. But since Alice has replaced it with another transaction that uses its same input, nodes will now consider Bob’s transaction invalid, because it’s referencing an already spent input.
Double Spend Prevention
So how does the ordering system prevent Alice from defrauding Bob? You might think that Alice could pre-compute a chain of blocks to spring on the network at just the right time, but the math puzzles in each block actually prevent this. We need to look a little deeper into the cryptographic hash explained earlier to fully understand why.
As mentioned previously, solving a block involves trying to get the cryptographic hash of the block to be below a certain value, and you do that by trying different random numbers at the end of the block. Once solved, the hash output is like a fingerprint that uniquely identifies that block. If even a single character in the block is changed, the block’s hash would be completely different, just like we saw before when an additional period was added.
The hash output, or fingerprint, is actually what’s used as the “previous block” reference. One result of this is that there’s no way to switch out a block in the middle of the chain, because the hash value for the new block would be different, and the next’s block reference would no longer point to it. And subtly, but even more importantly, a block cannot be solved before the previous block is solved. The previous block reference is part of the text that goes through the hash function, so any changes to it would require resolving.
Getting back to Alice, this is why she can’t precompute a branch. She can only start solving blocks once the block she wants to build on is solved, and its hash value is known. She is therefore in a race with the rest of the network until Bob ships a product, which is when she wants to present a longer branch. She must work in private, because if Bob heard about her double spend block, he would obviously not ship the product.One last question is whether Alice might be able to outpace everyone if she had an extremely fast computer, or perhaps a room full of computers. But even with thousands of computers, she would be unlikely to win the race to solve a block, because she isn’t racing any one computer, but rather the entire network. You can think of it like a lottery. She can operate thousands of computers, or equivalently, buy thousands of lottery tickets, but even then, it’s much more likely that someone else will win. She would need to control half of the total computing power in the entire network to have a 50% chance of solving a block before someone else. And much more to have a high probability of winning several blocks in a row faster.
So transactions in the block chain are protected by a mathematical race--one that pits an attacker against the entire rest of the network. A consequence of blocks building on top of each other is that transactions further back in the chain are more secure. An attacker would have to outpace the network for a longer amount of time to carry out a double spend attack, and replace a block. So the system is only vulnerable to a double spend attack near the end of the chain, which is why it’s recommended to wait for several blocks before considering received money final.
One last comment on the block chain before explaining the final pieces of the Bitcoin system. Amazingly, nothing described so far requires any trust. When you receive information from strangers in the Bitcoin network, you can check for yourself that the block solutions are correct. And because the math problems are so hard, you know that there’s no way any attacker could have generated them on their own. The solutions are proof that the computing power of the entire network was brought to bear.
Mining and Pools
Now that we’ve discussed how money is transferred through Digital Signatures and transaction chains, and how the order of those transactions is protected in the Block Chain, let’s go over the final piece: where Bitcoins come from. To send money, you must reference a previous transaction where you were the recipient, but how do coins get into this ownership chain in the first place?
As a way to slowly and randomly generate and distribute coins, a “reward” is given to whoever solves a block. This is why solving blocks is called mining, although its real purpose is to verify transactions, and safeguard the block chain. Every 4 years, the block reward is cut in half, so eventually no more coins will be released--about 21 million in total will be created. Bear in mind that you can send down to 1 / 100 millionth of a Bitcoin (.00000001), so the total number available will likely not limit the currency’s usability.
Once the block rewards cease, what incentive will miners have to process transactions? In addition to the block reward, miners also get any transaction fees that can optionally be included with transactions. Right now, miners will include transactions with no fees into blocks because their main incentive is the block reward, but in the future, transactions will likely be processed in order of the fees attached, and ones without fees will likely be ignored. So sending money in Bitcoin will probably not be free, but will hopefully still be cheaper than current credit card fees.
Mining Pools
As mentioned before, on average, it would take several years for a typical computer to solve a block, so an individual’s chance of ever solving one before the rest of the network, which typically takes 10 minutes, is very low. To receive a steadier stream of income, many people join groups called mining pools that collectively work to solve blocks, and distribute rewards based on work contributed. These act somewhat like lottery pools among co-workers, except that some of these pools are quite large, and comprise more than 20% of all the computers in the network.
The fact that some of these pools are so large has some important implications about security. As mentioned before, it’s very unlikely for an attacker to solve several blocks in a row faster than the rest of the network, but it is possible, and the probability increases as the attacker’s processing power gains in proportion to the rest of the network. In fact, one of the mining pools, BTC Guild, has solved 6 blocks in a row by itself, and has voluntarily limited its members to ward off distrust of the entire bitcoin network.
Even with substantial computing power, the farther back in the block chain a transaction gets, the harder it would be for an attacker to change it, as they must outpace the rest of the network for the time between when a transaction is sent, and when a product is shipped.
The current recommendation is to wait for a transaction to make it into at least one block, or get one confirmation, before considering it final. And for larger transactions, wait for at least 6 blocks. In light of BTC Guild’s ability to solve 6 blocks in a row, you might want to wait even longer.
Confirmation Time
By design, each block takes about 10 minutes to solve, so waiting for 6 blocks would take about an hour. Compared to the several seconds a credit card transaction takes, waiting this long for a confirmation may seem burdensome, but keep in mind that credit card customers can claim a stolen card months later to have charges reversed from merchants (called charge backs), so Bitcoin is actually much faster from a merchant’s perspective.
Why 10 minutes per block? The particular choice of 10 minutes was somewhat arbitrary, but extremely short times could lead to instability, and longer ones would delay confirmations. As more computers join the network, and specialized hardware is designed specifically for mining, the block solution time would get very small. To compensate, every two weeks, all the Bitcoin software recalibrates the difficulty of the math problem to target 10 minutes. For comparison, a similar digital currency called Litecoin has been able to operate with a 2.5 minute block time.*
*a paper by M. Rosenfeld, Analysis of hashrate-based double-spending, concludes that security is a function of the number of blocks, and not the time used to solve each block, but this assumes an attacker’s computing power is not dependent on time, ie, he could overpower the network for days just as easily as a few minutes.
*also see comments by Satoshi in this forum post regarding block time and system efficiency: https://bitcointalk.org/index.php?topic=130222.60
Conclusion and Summary of How Bitcoin Works
In summary, Bitcoin is a mathematically protected digital currency that is maintained by a network of peers. Digital Signatures authorize individual transactions, ownership is passed via transaction chains, and the ordering of those transactions protected in the Block Chain. By requiring difficult math problems to be solved with each block, would-be attackers are pitted against the entire rest of network in a computational race they are unlikely to win.
Bitcoin promises many interesting ideas, such as insulation from government meddling, anonymity, and potentially lower transaction fees. It also has many challenges, as it is currently very difficult to exchange Bitcoins for other currencies, and it has been cited as a haven for illegal activity and tax evasion, so governments may try to ban it. Also, the mathematical race that protects the Block Chain uses a substantial amount of electricity.
Bonus: Digital Signature Math
As explained above, a Digital Signature allows me to prove I have a private key, and that I used that private key to sign a particular message, without ever revealing my private key. Here is a simplified method, that, although insecure, shares some of the structure of a real Digital Signature Algorithm: RSA.
Consider the following variables:
p = public key
q = private key
p*q = N also publicly shared
m = message
if I make a signature from the private key and message, say, s = q*m, then a third party can verify the signature is mine by checking s*p = m*N. This is because
m*q*p = m*N, and N = q*p.
In this way, the third party only needed to know the publicly available public_key, N, message and signature. The only downside of this technique is that someone who knows how to divide would be able to calculate my private key by q = N / p. The real math falls under the umbrella of abstract algebra, and involves modular arithmetic, and our inability to factor extremely large numbers. Consider N = q*p, where q and p are large primes (300+ digits). Given only N, finding q and p would require vast amount of guessing and checking, but knowing q beforehand allows you to find p with simple division. This factorization trap door is what enables the RSA algorithm. The public key / private key algorithm used in Bitcoin is called Elliptic Curve DSA, and is based on the difficulty of finding a discrete logarithm. ECDSA’s advantage over RSA is that the key size required for a given amount of security is much smaller.
























The links to the last pictures are dead, for the rest excellent article.
ReplyDeletewill be adding lots of graphics from the video. Wanted to provide the script from the video, but will eventually make this blog post useful on its own.
Delete+1
DeleteScott, could you update please pictures/links? There are 4 dead pictures...
+1
DeleteWell-thought out and informative, best article/video on bitcoin I've come across.
Great tutorial..thanks
ReplyDeleteGood video!
ReplyDeleteDo you want to have Persian subtitle for Iranian? It can help you to have more visitors .
ReplyDeletePlease provide me the subtitle for this video.
We can cooperate with each other.
Please send an email to info at poolfa dot com
or admin at poolfa dot com
Thanks
Poolfa
How does this differ from how Litecoins work?
ReplyDeleteI believe the main difference is that the hashing algorithm has some extra "memory-hard" requirements that don't give custom ASICs the advantage over normal GPUs that they do for Bitcoin. Both Bitcoin and Litecoin's security rely on distributing the transaction verification process widely so no one entity can control the network. (I believe the large mining pools may compromise this). ASICs also have the potential to dis-incent people without ASICs from mining, which also concentrates the pool of verifiers. Note that the hash is still cryptographically just as hard in Litecoin as in Bitcoin, because it's actually just wrapping the same NSA provided SHA256 algorithm. Google scrypt.
DeleteAnother difference is that the block time for Litecoin is 2.5 minutes vs Bitcoin's 10 minutes. They claim this leads to faster confirmations, but only if you're satisfied with a few confirmations. If you're truly worried about a double spend attack, the total *time*, not raw number of confirmations is what protects you (not everyone will agree with this). So you should probably wait an hour with either network.
Thanks for all of this, im writing a report on cryptocurrencies and the comparison between the three leading ones. This helps alot.
DeleteHi Scott
ReplyDeleteGreat work. Thank you..
I was looking for a good bitcoin tutorial for a Turkish bitcoin auction webpage. (www.bitkoyun.com) I am planning to translate your work in Turkish with a link back to your blog page so my users could benefit of it is OK for you. Please reply to my email address.
Best wishes
bitkoyun@bitkoyun.com
Hi, great post! (note, not every image renders if browsing with IE09 - yes i know ... IE)a pdf "script" would be ... excellent! keep up the great work! k
ReplyDeletethe block signature guessing scheme does not really make much sense. it assumes that all the participants in the network are benign and operate according to the protocol. but if I have the ability to simultaneously hijack N computers in the network where N is equal to the number of broadcasting nodes to verify a transaction, I can easily create a chain of Txn, and by opening releasing the answer to the guess among these N hijacked nodes, I could grow my chain much faster, and then I'll release this chain onto the proper network, thus destroying all legal transactions.
ReplyDeletesince the above scenario seems to have never happened, where am I wrong in the above description?
Scott-
ReplyDeleteTHANK YOU for this most informative and well organized video.
Can you please clarify/confirm the following conclusions:
1. Blocks need unconfirmed transactions => If, theoretically there were no new transactions for a while, no miner would not be able to create a blocks at that time.
2. No blocks will be creatable past some future time (currently estimated at year 2140) => No more Bitcoin transactions will be possible past that time. (I know this is far away, but I am sensitive to it: In 1986 people thought I was crazy because I was talking about the y2k challenge.)
Thanks again
re: blocks without transactions: I'm not sure, but I suspect you could create a block without any transactions and just have block header info in it.
Deletere: no blocks will be creatable past some future time: no block reward will be issued past 2140ish, blocks will still be created.
it seems that the block reward is itself the first transaction
DeleteWonderful and Excellent explanation of how Bitcoin works. Very straight forward examples and clear visual concepts to wrap one's brain around it. Would you consider doing another great video for the Timekoin currency? It has been going for years and uses a completely different model that many people confuse with Bitcoin.
ReplyDeleteSounds interesting, sounds like it doesn't utilize proof-of-work? Looking forward to understanding it more.
Deletesingle a finite variety associated with bitcoin mason have been created, in which helps make Bitcoins seem to possibly be added valuable when compared with they actually are.
ReplyDeleteI'm wondering what happens if a country or continent looses internet connectivity with the world for a longer period (hours, maybe weeks) ?
ReplyDeleteThe nodes in that country continue to generate blocks and would basically fork the blockchain, confirming all internal transactions.
Then, when connectivity is restored (assuming the global network has outperformed the isolated network and generated a longer blockchain), all transactions in the forked chain would become unconfirmed again.
What if an attacker has the capacity to turn off internet access for an entire country AND double spend the coins on the split networks (spend the same coin on the 'global' internet and on the 'local' internet) ?
What could you comment on that ?
That's a really interesting point. I can think of a few countries that might even want to do that on purpose.
Deleteno no no, this problem does not exist. in your case, the number of small portion of people ( people in the country) is less than outside, once the connection restored, all of your transactions will be dismissed and put into unconfirmed transaction list to be verified again, and finally they will all be verified and put into the global block chain later.
DeleteExcellent explanation man, thanks!
ReplyDeleteHi Scott. Thanks for this great article and video. I want to translate your work into Chinese as a tutorial. If it is ok with ,please let me know.THX!
ReplyDeleteThat would be fantastic, I'll link to it when you publish. Some day I'll get better graphics on this article. The graphics in the video are the only correct ones.
DeleteSerenenight: Please do!
DeleteScott: If ok, can you also publish in the comments. I have many Chinese friends, and I would like to send it to them.
Thanks
Sure, just let me know.
DeleteThanks a lot for the fantastic video! the best i have seen yet!
ReplyDeleteAwesome job. Thank you for the great video on YouTube and now the script! Jackpot.
ReplyDeleteWould it be alright if I used this material and translated it to Korean? Thanks. Want to get a verbal confirmation before I use your work.
ReplyDeleteThat would be great, let me know when you're done, and I'll put a link here.
DeleteCan you make a vid about complex transactions, i.e. msig transactions? what happens to the btc if nobody signs, for example?
ReplyDeleteHi Scott,
ReplyDeleteGreat tutorial, but I'm a little unsure of the following:
1) How is the order of transactions WITHIN the block determined?
2) Isn't it critical that the order of transactions WITHIN the block be exactly the order of when they took place. If Alice broadcasts two transactions with the same inputs (during a double-spend attempt), then if a miner creates a block to mine with TXa before TXb, when in reality TXb took place before TXa, then the double-spend attempt could succeed.
Can you please elabroate? thanks!
hi Scott, what's the secret to 0-fee transactions? setting "bitcoind settxfee 0" didn't work, I still got charged BTC0.0005 per transaction.
ReplyDeletealso, every nonce generator I've seen in cryptocurrency daemon sources are linear starting at 1 (though comments in the code indicate it should start at 0), so are not truly "random". I found out for sure today, though, that random numbers do actually work, at least for AmericanCoin.
Hi Scott,
ReplyDeleteThanks a lot for the video on youtube. It was really informative.
I wanted you to clarify this for me,,
When you talk about gold, it is rare and cannot be printed into existence. Also the number of precious metals like gold is limited.(platinum, silver and a few others at max). In the case of bitcoin even though bitcoin is limited in supply(21 million), virtual currency itself is not limited. One can easily make something like fitcoin, or the already existent litecoin.
Do you think this could have a negative impact on the potential of bitcoin to be a currency(the fact that the concept is easily repeatable)?
to ensure no double spending, bitcoin runs through a list of all unspent transactions instead of the list of all previous transactions? wouldn't that take much longer, considering that the transactions that have taken place to date are much much smaller than the total number of possible transaction codes - the grains of sand squared ?
ReplyDeleteGreat article, a detailed but not too technical explanation of Bitcoin. BTW some of your images below "The Block Chain: an Ordering of Transactions" are not showing up.
ReplyDeleteOtherwise awesome!
Great job! Nice post.
ReplyDeleteWow to you for your informative layout of bitcoin functions. I'm impressed with your explanation simplification of the process. You have a great mind you'll go far. Good job!
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThank you for this very informative video, do you have a video on btc mining hardware and set up?
ReplyDeleteSome of the pictures are not visible. If I try to open in new tab, Google drive says I need permission to access that, and gives me the option to request permission.
ReplyDeleteBTW, your video is the best explanation of bitcoin out there that I could find. I hope you continue to offer more great educational bitcoin videos.
thanks, Drew. Ask and receive! I just released a shorter, less technical version of this video: "How Bitcoin Works in 5 Minutes" https://www.youtube.com/watch?v=l9jOJk30eQs
DeleteHey Scott,
ReplyDeletehaving spent some time looking for educational videos for Bitcoin I think your one is by far the best when considering technical depth and clarity combined.
I have been tweeting it out: https://twitter.com/MrChrisEllis/status/456065829499842560
And I will continue to promote it. Let me know if you are planning any more.
thanks! I just released a 5 minute version, and am considering a 2 minute non-technical one, also.
DeleteMaybe I can release a 2 second version in Dutch.. ;-)
DeleteNo no just kidding... If you want to see in translated into Dutch (Belgium) just ask... It will be a good practise for me or my daughter who is studying for translator..
Scott,
ReplyDeleteI have search the internet looking for educational information on Bitcoin, and the transaction process of bitcoins. What you wrote is the best thing that I have found. Oh, let me not forget, your videos are pretty nice too. Thank you for clarifying and providing answers to a number of questions that I had.
Scott
ReplyDeleteBoth videos are awesome. Now that you are leading the explanations arena, can you please educate the world about this
*** The ONLY risk from bitcoin is when you own it/hold it, as its price could go down.
*** You can benefit from bitcoin without owning/holding any.
*** You can benefit from bitcoin without even understanding how it works!
Merchants need NOT own or understand bitcoin.
Merchants can simply employ a 3rd party processor (bitpay, coinbase, coinkite, coinsimple, others) to receive the bitcoin for them and return cash to them
Merchant benefits:
#1/ALWAYS: Negligible interchange fees, compared to credit cards.
#2/ALWAYS: No risk of bad payers (can't do that with bitcoin).
#3/ALWAYS: Get paid cash via ACH to your bank - FAST. Not several days later.
#4/Some times: If the merchant's upstream vendors give discounts for getting paid in bitcoin (because benefits 1, 2, and 3 ALWAYS apply to them as well), then these discounts go straight to the bottom line.
It is the merchants who gain from bitcoin. And they do not even need to understand the mechanics!
Scott
ReplyDeleteAfter having clarified that one does not need to understand bitcoin in order to benefit from it, could you please also add the following.
This is the same as the 5-minute video EXCEPT it has been scrubbed from all crypto terms
1. Where is bitcoin stored?
All Bitcoin balances are always stored in ACCOUNTs.
ACCOUNTs are public.
Anyone can always deposit to an ACCOUNT.
2. How is bitcoin transacted?
Transactions send bitcoin from one ACCOUNT to another ACCOUNT.
Transactions are stored in a file called the blockchain.
In order to create a transaction the sender must have the PASSWORD for the ACCOUNT.
PASSWORDs are private to the holder
All of the above is handled by software called bitcoin WALLETs.
3. Who defines the ACCOUNTs and PASSWORDs?
ACCOUNTs and PASSWORDs come in pairs.
There exists ONE-WAY MATH that operates as follows: PASSWORD + [ONE-WAY MATH] => ACCOUNT
For every PASSWORD there is one and only one ACCOUNT, and can be easily calculated via the ONE-WAY MATH
For every ACCOUNT there is one and only one PASSWORD, and can NEVER be calculated, because the ONE-WAY MATH cannot be reversed.
So the question is really "who defines the PASSWORDs?" (because each PASSWORD defines its corresponding ACCOUNTs)
4. OK! How are PASSWORDs defined/created?
There are quintillions of possible PASSWORDs.
The WALLET software can create them at random.
Alternatively, people can crete them with algorithms and keywayrds (via places like brainwallet.org)
5. What guarantees safety?
5.1 re the ONE-WAY MATH
The ONE-WAY MATH is based on cryptography.
The prize for figuring out how to reverse it is $5bn (today's value of the blockchain).
The best mathematicians in the world cannot figure out how to reverse it. If they could, they would get $5bn.
There is no secret in a vault anywhere: The ONE-WAY MATH is public!
5.2 re PASSWORDs
PASSWORDs cannot be guessed: This requires lucky odds trillions of times betten than winning the lottery.
But people do lose their bitcoin on occasion
* trust them to incompetent or fraudulent 3rd parties
* misplace their PASSWORDs
* allow their PASSWORDs to be copied by
- storing them electronically in unsecure places (e.g. in computers that can be hacked), or in wallets with weak wallet passwords
- storing them on paper in unsecure places (e.g. bank safety deposit boxes)
- transmitting them unencrypted (e.g. via email, skype)
* allow their PASSOWRDS to be reverse-engineered easily by creating them with common keywords (e.g brainwallet.org)
7. Using a WALLET:
WALLETs enable the user to receive, spend, see their balance etc.
You need to learn these new terms:
Wallet softwares does not talk about ACCOUNTs. Instead they refer to ACCOUNTs with the cryptographic term "public key".
Wallet softwares does not talk about PASSWORDs. Instead they refer to PASSWORDs with the cryptographic term "private key".
Maybe future wallets will use the easier terms
Lots of good suggestions, John. I'll take those into account in my next 2 minute version :)
DeleteHello,
ReplyDeleteI would like to translate your video https://www.youtube.com/watch?v=Lx9zgZCMqXE into Czech language.
If this is possible, could you please supply me with some .srt files? Not sure how the translation on YouTube works, Thanks.
There is a huge misconcept on the probability curve showing the of solving the puzzle, vs. time, The probability will allways increase!, as more and more chance is given to solve it, due to elapsed time, it does never decrease after 10 minutes! (its not a probability distribution) which might be the mistake!
ReplyDeleteBitcoin is the best digital currency one could really look forward towards. But the main thing is that it's not legal and there are a few people who are not interested in Bitcoin being legal.
ReplyDelete@Scott,
ReplyDeleteI am a High School teacher and I would like to do a class on bitcoin/crypto-currency. I want to use a very, very simple example of a encryption function so that students could create signatures from a private key and a message. I could then post those messages/signatures and they would see quickly that they can only "unlock" the messages that they already have the private keys for. Even if the function is very weak for a computer, I just need something plausible for a student with a calculator to be able to do so that they cannot readily reverse the logic to determine the private key.
Got any of those?
The best thing I can recommend is the "Digital Signature Math" at the bottom of the article...
Delete@Scott,
ReplyDeleteI am a High School teacher and I would like to do a class on bitcoin/crypto-currency. I want to use a very, very simple example of a encryption function so that students could create signatures from a private key and a message. I could then post those messages/signatures and they would see quickly that they can only "unlock" the messages that they already have the private keys for. Even if the function is very weak for a computer, I just need something plausible for a student with a calculator to be able to do so that they cannot readily reverse the logic to determine the private key.
Got one of those?
James
DeleteI don't know if this helps, but here you go:
In the simplest form, you start with a SEED. (For Bitcoin this is the account password, which you can create, or have the wallet create for you).
The FUNCTION starts with the SEED and generates the RESULT. (For Bitcoin this is the Bitcoin account).
Many functions are reversible, where you can start with the RESULT and get the SEED.
Example Reversible Function: RESULT = SEED + 3
So, if SEED=4, RESULT=7.
And to reverse, SEED = RESULT - 3 = 7 - 3 = 4.
For Bitcoin the functions are irreversible. You create the account by applying 4 such functions in a row.
To see them all together look here: https://www.bitaddress.org/
Separated the 4 functions are:
Memorable Text=>SHA256Digest
SHA256Digest=>Bitcoin Password (aka private key)
Bitcoin Password=>Public Key
Public Key=>Bitcoin Account.
To see these function separately coded as Excel functions in Visual Basic, you may review this: http://bitcoinspreadsheet.blogspot.com/p/wallet-programming-contest.html. Caveats: 1. Visual Basic is a very inefficient language for this, so it will take A VERY LONG TIME for the cells to refresh. It has been created for demonstration purposes only. 2. The contest prizes mentioned are no longer offered. 3. The spreadsheet should be usable as a wallet, but has not been vetted. (Despite the large prizes, programmers did not want to confirm it.)
Hope this helps,
John
Hi Scott, thank you for your time to make these videos. After reading the manuscript from Nakamoto I'm trying to understand your explanation about the guessing part.
ReplyDeleteWhen you talk about the cryptographic hash in the blockchain ordering of transactions part, you imply that every computer in the network (the so called miners) are all guessing what the answer is. So am I correct if I say every miner is not calculating anything but just guessing the answer. The possibility of finding it is so exponentially small you could say the system therefor depends on the statistical chance of luck.
Still, although there is this extreme tiny chance of finding the solution, finding the solution 7 or 8 times in a row is even more rare to near impossible. You agree?
Hope you find the time to clarify this.
Thanks in advance
this is correct, solving the problem is akin to rolling dice. Rolling a 6 several times in a row is less likely than just once.
Delete"So, instead of a ledger of balances, Bitcoin nodes keep track of a giant list of transactions. Owning Bitcoins means that there are transactions in this list that point to your name, and haven’t been spent, or, in other words, used as inputs in other transactions."
ReplyDeleteWhat about the transactions with 2 outputs? One output to pay someone and one output with the change, pointing to my address? This transaction has to be used twice ... or do you mean, that just every output entry has to be used once?
Thanks for your answer ;)
Excellent video. ECDSA link is giving "Database Error...". http://kakaroto.homelinux.net/2012/01/how-the-ecdsa-algorithm-works/
ReplyDeleteImpressive post.
ReplyDeleteHi Scott,
ReplyDeletethanks for creating that good video. It helped me to understand how Bitcoin works, but I still have one question.
You said, that you need to find the correct random number of the current block to be allowed to add your block. But with adding your block you actually know the random number of the new last block. So you can easily "guess" it and add another and another... What did I get wrong?
Thanks,
Peter
Let me try to define terms a little more precisely. By random number, I mean the nonce that goes into the hash function for the current block you're trying to solve along with the hash for the previous block and transactions. The full result of that hash needs to be smaller than the current target. So, h(last_block_hash, nonce, transactions) < t. The random number for the last block isn't involved.
DeleteSo BitCoin actually uses TWO blockchains? One for the transactions and one for the order of the Blocks? AND: When a signature gets validated, it's transaction will be added to the transaction blockchain? And later added to a block which is added to the chain?
ReplyDeleteGreat article! It helped me a lot to understand how Bitcoin works deeply. Thanks!
ReplyDeleteVery nice. Putting the course on pluralsight is not as nice though. Any site which promotes "learning for free" and asks your financial details on the second page is not to be trusted IMHO.
ReplyDeleteWould be happy to follow (and pay for) the course on a pay-per-use basis....
Unfortunately PS only has a subscription model right now. I'm pretty sure there's no "learning for free" suggested anywhere, except that you can get a free trial.
DeleteHi Scott,
ReplyDeleteFirst of all the best article i found on Internet on Bitcoin.
I have few queries.
Request you to please throw some light on it:
- Lets say Alice sends money to Bob. ( The transID is xxxxxx )
The value of PrevOut (Previous transaction from where Alice got the money) is say yyyy.
- The transaction(xxxx) gets broadcasted and selected lets say in the latest block in the blockchain.
- Now after few successive blocks (lets say 10 blocks) Alice creates a new transaction(zzzz) indicating payment to a different user called David and uses the same old transID as the value of PrevOut (yyyy) and broadcasts it.
My questions are:
- How does the miner now that this transaction(yyyy) has already been used 10 blocks ago ? Of course he can use the transaction chain to identify that this transaction was present in a block which is 10 block behind the current block but since there will be so many transactions must have happened in those 10 blocks the miner will get to spend immense amount of time to validate it. In your blog you mentioned that it takes 24 hours to validate the complete block chain. So during a new block creation how much time it takes a miner to typically validate that a new trasaction's prevOut value is not present in all the previous blocks ?
Excellent Article. Very helpful. Thanks.
ReplyDeleteQuestion - How does the target (or threshold) gets determined?
it's adjusted to maintain a 10 minute block time automatically. Find out all the gory details: https://bitcoin.org/en/developer-guide
DeleteThanks
DeleteHi Scott, this is a great video. Do you have any other material to explain ethereum on same lines - how does smart contract work on blockchain?
ReplyDeletethis video gives me a lot insight of Bitcoin. much thanks!
ReplyDeletefew questions:
1. as block chain is a distributed ledger on each node, then how much data space does each node need? sounds enormous!
2. will there some 'digital discrimination' on Bitcoin, due to slow network connection and less computing power?
3. in your article, a new bitcoin user need to download Bitcoin wallet, and download every transaction ever made in history and ... if the new user found some transaction invalid, what will happen to him/her and to the whole Bitcoin users?
4. what's the back-end algorithm to keep the '10 minutes' verification time?
5. when a node finds another longer chain out there, then it will switch to it. how does a node compare its chain length with another? because there will be tremendous fork chains out there, how long will it take to cross compare all of them?
6. the last question, transaction confirmation. you say it's better to wait 1 up to 6 blocks to make the final confirmation. it seems unacceptable and the most weak point for bitcoin. let's say if there is no new transaction at the time, well the last transaction block can be manipulated arbitrarily by the most powerful person/machine?
I have a problem understanding Double Spending in Bitcoin. As if i have 5BTC and i made a transaction of 5BTC to some other person my BTC will be now 0. Then how i could make another transaction thats not possible and also once the transaction is made there no way it can be cancelled please reply asap.
ReplyDeletethankyou
Transactions don't confirm immediately, and it's in that window before they confirm that there's a risk of double spending.
DeleteProbably THE best explanation out there.
ReplyDeleteWonderful work. Keep it up.
P.S: If interested in having it translated to Arabic, I would gladly do it. Just reply here :)
Cheers, and thanks again
How is it possible for every user to store that huge database of all the transactions ever made? It should be hundreds or even thousands Gb and growing.
ReplyDeleteonly miners / bookkeepers store the transactions. It is hundreds of GB and growing--it's a concern.
DeleteHi Scott,
ReplyDeleteBy far the best explanation I found. Well written, Thanks.
One question:
1) How the order in the block is determined? What if Alice makes one more transaction to another party and it goes into the same block and before Bob's transaction.
What is preventing this from happenning?
Within block order is determined by miner that creates block. Two transactions from valid one party are valid within one block as long as they don't break any rules. Blocks are checked for validity before being accepted by other miners, so it would be useless to create an invalid block. Winning the race to find the hash only pays out if your block is accepted.
ReplyDeleteGreat explanation, thank you.
ReplyDeletewhat are the effects or consequences when a bitcoin is / will be backed by real assets like the Petro in Venezuela and the yuan in China. more stability !!!
ReplyDeleteAmazing video. Well done !
ReplyDelete